Définition
Sphérique à doigt
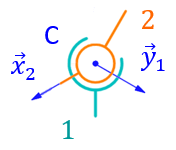
de centre C, d’axe (C,\vec{x}_{2}) et de normale \vec{y}_{1}
Famille
Liaison à centre
Caractéristiques géométriques
Dans l’espace 1, il existe le point C_{1}.
Dans l’espace 2, il existe le point C_{2}.Les deux points restent coïncidents.
Torseur cinématique
\overrightarrow{V}_{2/1} =\begin{matrix}\\ \\ C\end{matrix}\begin{cases} \overrightarrow{\Omega}_{2/1} \\ \vec{0} \end{cases} avec \overrightarrow{\Omega}_{2/1}.(\vec{x}_{2}∧\vec{y}_{1})=0
Torseur des actions mécaniques
\overrightarrow{M}_{1→2} =\begin{matrix}\\ \\ C\end{matrix}\begin{cases} \overrightarrow{R}_{1→2} \\ N_{12}\vec{x}_{2}∧\vec{y}_{1} \end{cases}