Joint de Cardan

Définition

Un joint de Cardan est un accouplement mécanique, c’est-à-dire qu’il transmet un mouvement de rotation entre deux arbres. Si le joint de Oldham permet d’accoupler deux arbres dont les axes de rotation sont parallèles, le joint de Cardan permet d’accoupler deux arbres dont les axes sont concourants.

Il présente le défaut d’être hétérocinétique, ce qui signifie que la vitesse de rotation des deux arbres autour de leurs axes respectifs n’est pas la même à tout instant. Pour palier à ce défaut, on utilise les joints de Cardan par deux :

Modélisation

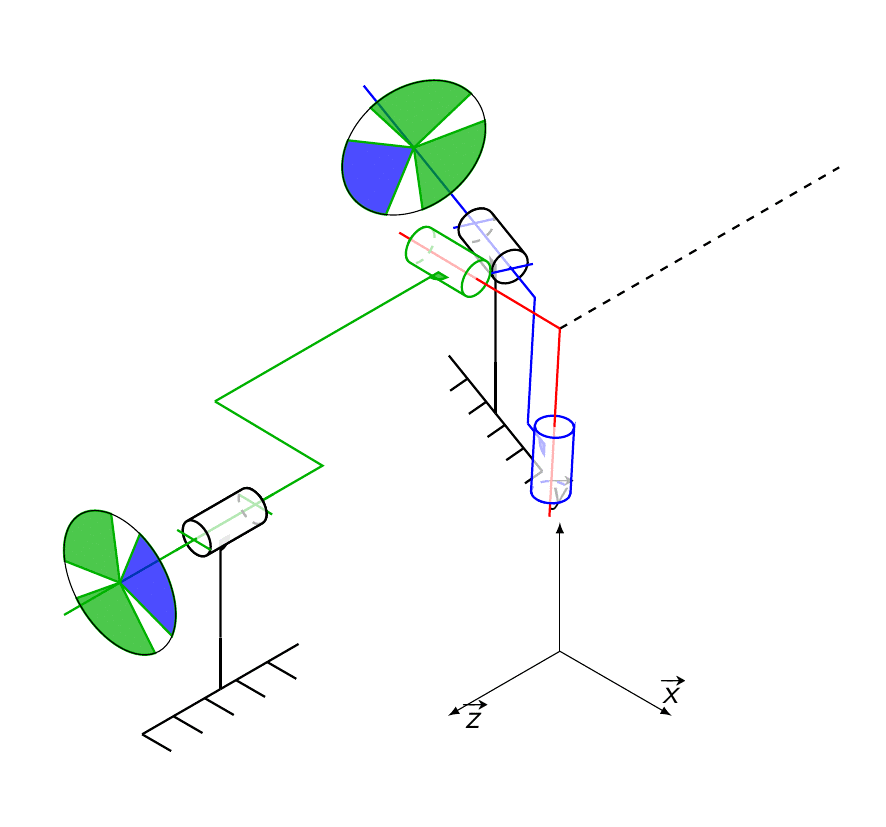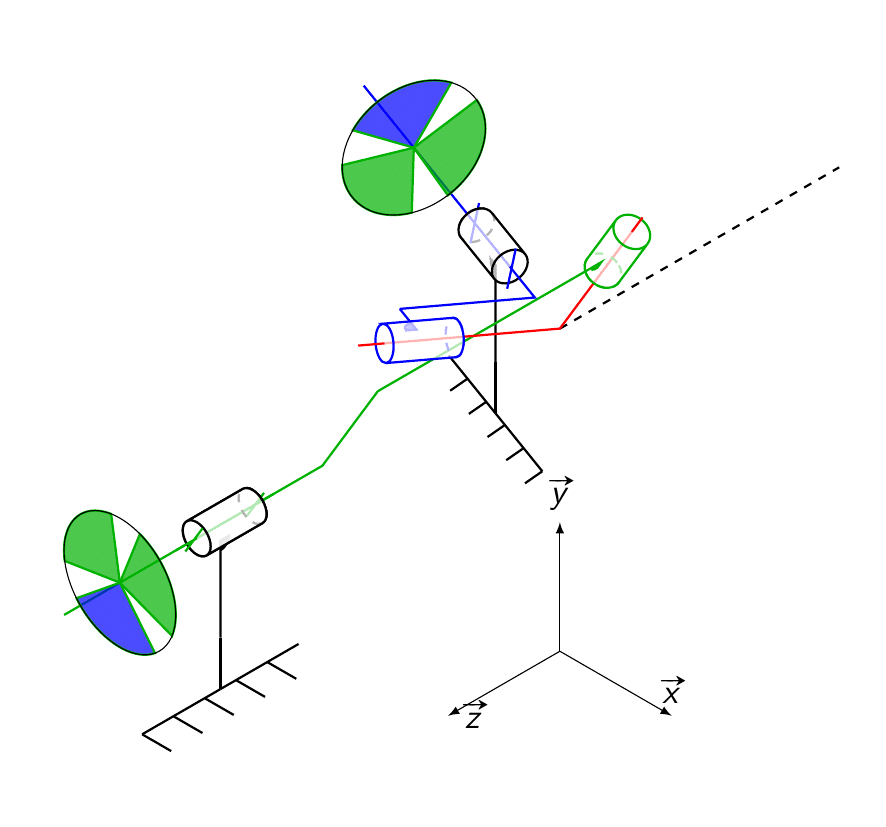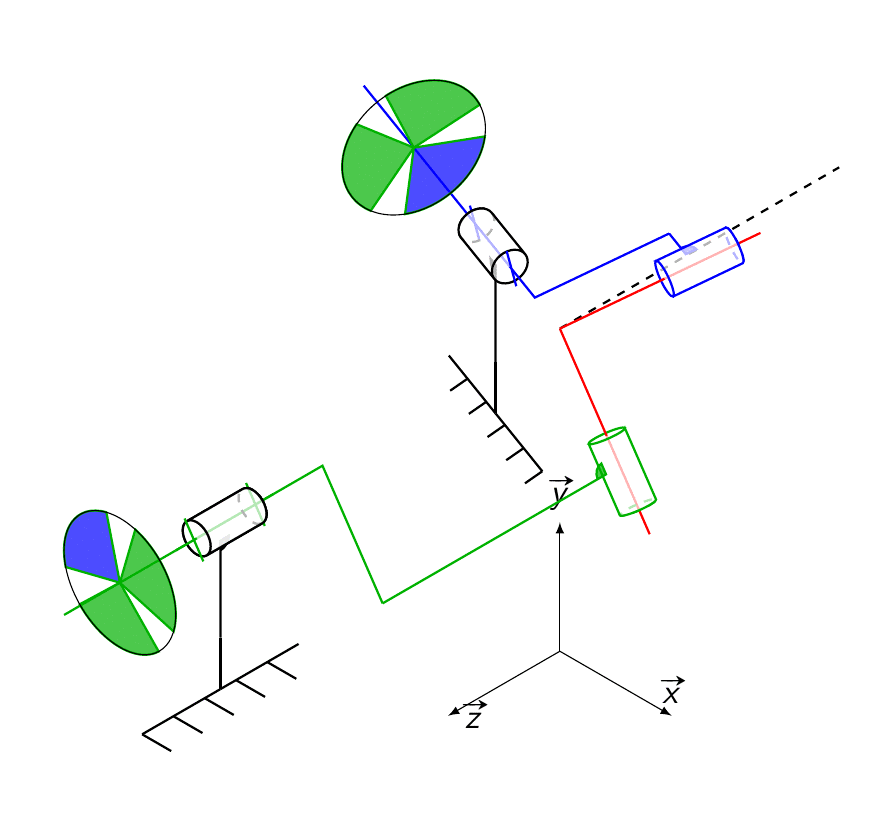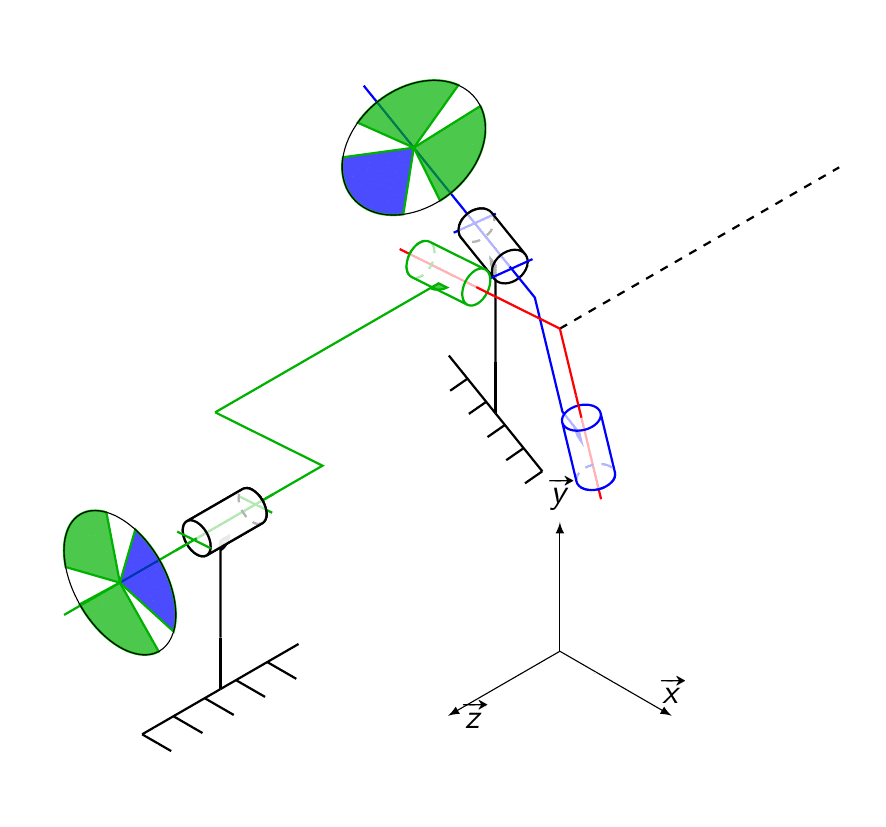
La relation entre la rotation des deux arbres dans le cas d’un unique joint de Cardan est dépendante de l’angle entre les deux axes. Voici le schéma cinématique du joint de cardan. L’arbre d’entrée entraine l’arbre de sortie incliné d’un angle \alpha, par l’intermédiaire du croisillon :

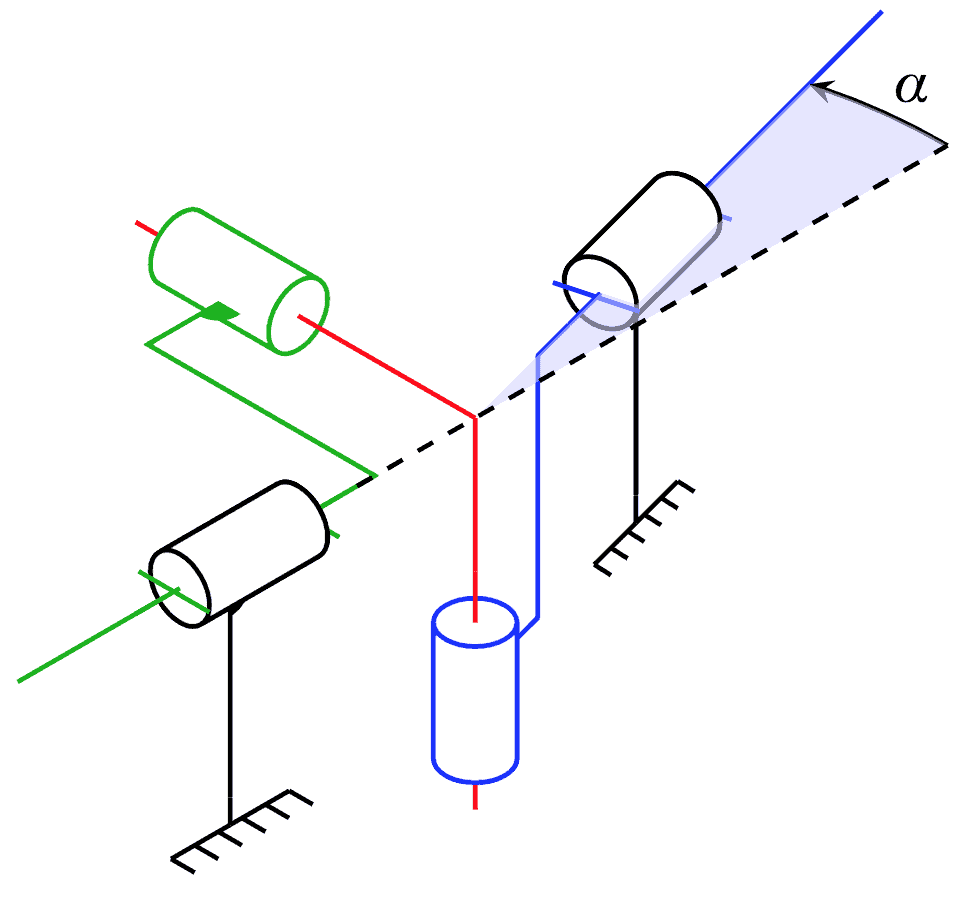
À l’aide de la perpendicularité apportée le croisillon, on peut trouver la relation :

\tan(\theta_{10})\cos(\alpha) = \tan(\theta_{20})

où \theta_{10} est la position angulaire de l’arbre d’entrée et \theta_{20} de l’arbre de sortie.

On trace la loi d’entrée-sortie \theta_{20} en fonction de \theta_{10} :

On remarque que les positions angulaires se rejoignent périodiquement tous les 90°, évidemment les deux arbres font le même nombre de tours en moyenne, mais pas exactement en phase. Plus alpha est grand, plus les différences sont grandes. Ces oscillations peuvent déjà poser problème pour un système où le positionnement a un rôle critique, mais les problèmes sont plus visibles encore si l’on étudie la vitesse de rotation :

  \displaystyle\frac{\dot{\theta}_{20}(t)}{\dot{\theta}_{10}(t)} = \frac{(1+\tan^2(\theta_{10}))\cos(\alpha)}{1+\tan^2(\theta_{20}) }
ou
\displaystyle\frac{\dot{\theta}_{20}(t)}{\dot{\theta}_{10}(t)} = \frac{\cos^2(\theta_{20})\cos(\alpha)}{\cos^2(\theta_{10}) }

Si on trace le résultat on obtient :

Sur la courbe de ce tracé du rapport des vitesses de rotations, les différences sont beaucoup plus visibles pour les mêmes valeurs de l’angle \alpha que le tracé précédent. On remarque que le rapport de transmission a une valeur périodique (de période 180°).

Ces variations induisent une augmentation de la vitesse de rotation maximale, mais surtout impliquent la présence de vibrations qui peuvent être néfastes aux systèmes.

Si l’on fait tendre la valeur de \alpha vers 90°, le rapport tendra à prendre des valeurs proches de zéro sauf pour un pic (au voisinage de \theta_{10} = 90° ou 270°) tendant vers l’infini. Comme si un arbre restait immobile pendant que l’autre tourne, et que tous les 180° de l’entrée, la sortie bondissait d’un demi-tour instantanément pour la rattraper. On comprend donc que cette valeur est inutilisable et on évite de s’en approcher.

D’après la formule du rapport de transmission on peut voir que dans le cas général, le joint de Cardan n’est pas homocinétique, mais le devient si \cos\alpha = 1 , ce qui donne \alpha = \pi et \alpha = 0, le premier cas n’est pas possible à cause des collisions des pièces et le deuxième cas la présence du joint est superflue.

Voici le schéma cinématique animé pour un \alpha de 70°, des roues sont ajoutées pour bien constater que quand l’arbre d’entrée tourne à vitesse de rotation constante, celle de l’arbre de sortie ne l’est pas.

Montage en pratique

Monté seul, il est hétérocinétique, il est donc en général monté par deux, pour être homocinétique (le montage à deux joints permet une transmission homocinétique seulement si les deux ont le même \alpha. Ils peuvent être montés en Z ou en W selon leur orientation. L’angle \alpha ne peut pas atteindre 90°, et même au delà de 45° un joint de Cardan particulier est nécessaire.

Montage en Z en haut et en W en bas