Définition et notations
Définition
On appelle engrenage l’entraînement de deux solides par des dentures.
Engrenage sans transformation de mouvement
 |  |  |  |  |
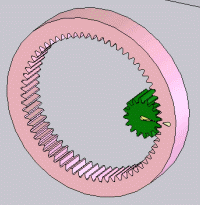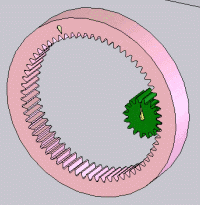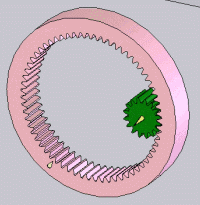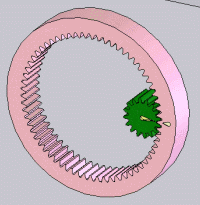1 engrenage qui se compose d’un petit pignon et d’une grande roue à denture droite | 2 pignons à denture hélicoïdale | Renvoi conique | 1 engrenage à contact intérieur composé d’une couronne et d’un pignon | Roue-vis |
 |  | |||
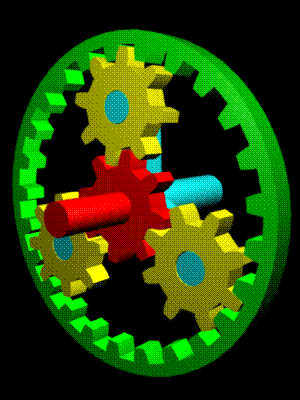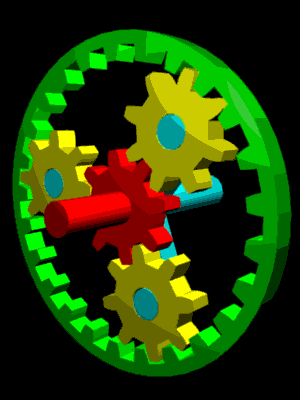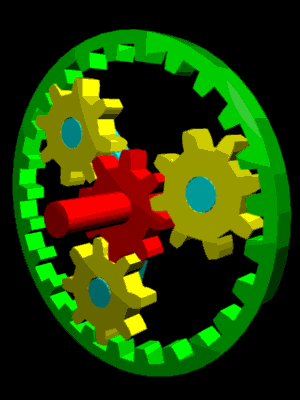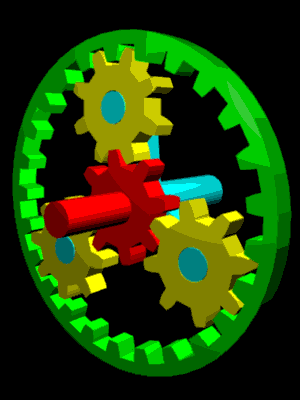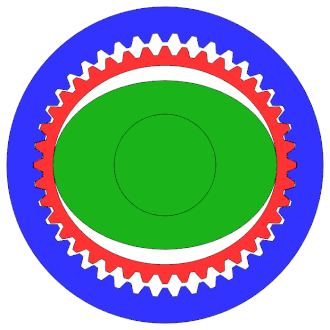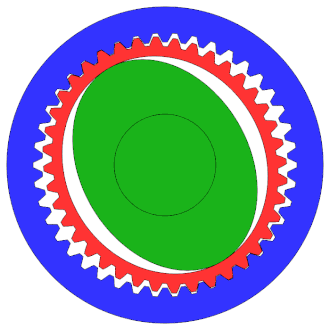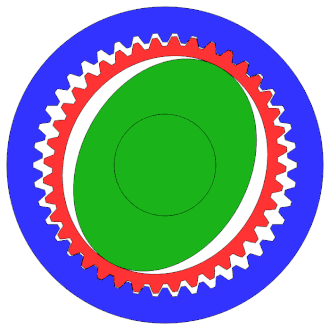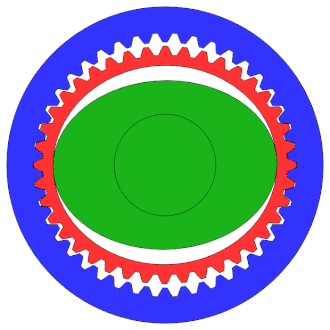Train épicycloïdal | Harmonic Drive |
Engrenage avec transformation de mouvement
|  |  |
Pignon-crémaillère | Vis-écrou | Pignon-chaîne |