Comment peut-on mesurer une action mécanique ?
Capteur à jauges de déformation
Les jauges de déformation sont utilisées pour réaliser un « capteur de force ».
Ce sont de petits circuits électronique en labyrinthe que l’on colle sur la surface d’une pièce qui se déforme. En mesurant la tension au borne du circuit, on en déduit l’action mécanique qui a été appliqué.

On les met dans un pont de Wheatstone. L’association des quatre jauges en pont complet permet de rendre le montage quasiment indépendant aux efforts parasites
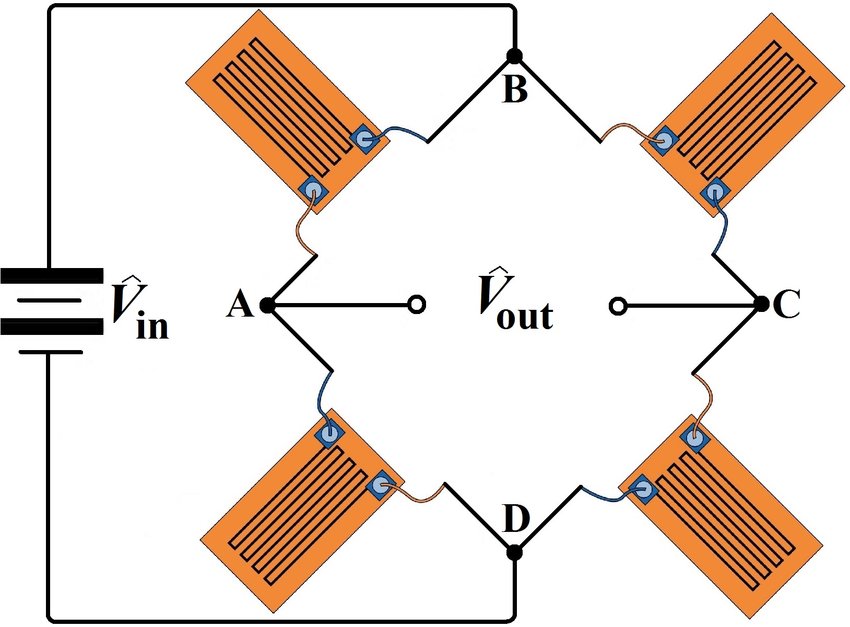
On colle ce pont sur une structure en S déformable. En perçant deux trous, on s’assure d’une déformation uniforme au niveau de la surface, ce qui permet de positionner facilement les jauges.
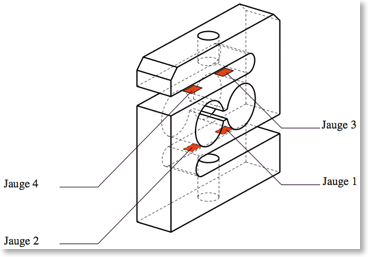
Support de l’étude proposée
On souhaite étudier le comportement d’une cellule d’effort utilisée sur de nombreuses machines d’essais. La cellule considérée utilise un pont de jauges de déformation placées dans une configuration bien particulière sur un corps d’épreuve. Logiquement, les jauges sont placées dans les zones présentant les déformations les plus importantes : nous le vérifierons lors du calcul.
Principe des jauges de déformation
Les jauges de déformation sont des circuits résistifs dont la résistance varie avec la déformation. On sait tout d’abord que la résistance du fil est donnée par :![]()
où interviennent la résistivité, la longueur, la section, et le volume du conducteur.
Ainsi, on obtient :
![]()
La résistivité ρ est une constante électrique fonction de l’état de déformation du conducteur. Cette fonction est modélisée par la loi de Bridgman :![]()
Ceci conduit donc à :![]()
Pour un conducteur à section rectangulaire, le volume V et sa variation relative sont donnés par :![]()
Dans le cas d’une jauge de déformation collée à la surface d’une structure dont le coefficient de Poisson du matériau est noté υ, les déformations longitudinales et transversales sont liées par :![]()
Ainsi, on obtient les deux relations suivantes :
et donc :![]()
En injectant cette dernière expression dans l’équation donnant la variation relative de résistance, on obtient :
Finalement on a donc montré que la variation relative de résistance était reliée linéairement à la variation relative de longueur du conducteur, c’est à dire à la déformation longitudinale :![]()
On note k le facteur de proportionnalité, et on le nomme facteur de jauge. Ce facteur est fourni par le fabricant de la jauge.

Le paragraphe précédent a montré que la déformation longitudinale était proportionnelle à la variation relative de résistance du conducteur (généralement très faible). La mesure de la variation relative de résistance peut se faire par une mesure de la tension de déséquilibre d’un pont à quatre résistances de valeurs voisines, préalablement équilibré à la mise en charge de la structure équipée de jauges. Un calcul simple donne la relation entre la variation δe et les variations relatives de chaque résistance :![]()
En pratique le déséquilibre δe du pont est inférieur au millième de Volt et il est nécessaire, pour le mesurer à l’aide d’un millivoltmètre, de recourir à des amplificateurs de gain G. Finalement, on mesure donc le potentiel Vi :![]()
Modélisation numérique
La CAO du capteur d’effort a été créée en prenant des mesures, le plus précisément possible, sur un capteur existant. Le maillage est constitué d’éléments tétraédriques (linéaires, mais on aurait pu choisir paraboliques). Le chargement correspond à de la traction sur le corps d’épreuve. L’alésage inférieur a été encastré, un effort est imposé, via une pièce virtuelle rigide sur l’alésage supérieur.

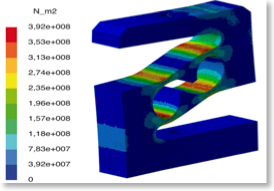
Pour un maillage donné, il est préférable de tracer la contrainte de Von Mises brute issue du calcul, c’est-à-dire au points de Gauss des éléments, plutôt que son analogue lissé. Le champ est représenté sur la figure ci-contre. Le maximum obtenu pour un chargement de 1000 N en traction est de 400 MPa. Cette contrainte semble un peu élevée pour un aluminium (à affiner en fonction de la nuance). La charge de 1000 N est sans doute au delà de la charge limite tolérable par ce capteur.

On souhaite récupérer les évolutions des déformations sur les arêtes rouges représentées sur la figure ci-contre afin de les comparer aux résultats obtenus par une modélisation simplifiée du capteur présentée dans le paragraphe suivant. Pour cela on définit deux groupes de lignes ayant comme support les arêtes supérieure et inférieure. On restreint ensuite le tracé du champ de déformation (composante C11) à ces deux groupes et on exporte les résultats dans un fichier texte afin de comparer les résultats à la modélisation simplifiée présentée ci-après dans un tableur.
Modélisation analytique simplifiée
La modélisation simplifiée est présentée sur la figure ci-contre. On considère que seule la zone centrale, autour des perçages se déforme et que le reste du capteur est parfaitement rigide. On fait l’hypothèse que les lames sont d’épaisseur constante égale à e=2,5mm : il s’agit de la plus faible épaisseur du voile sur le capteur. La longueur des lames est définie par la longueur L retenue sur le plan du capteur. L’équilibre d’une lame se traduit par :![]()
et![]()
L’équilibre de la partie rigide supérieure donne :![]()
Les moments fléchissant dans les deux lames sont donc :![]()
Le système ne présente aucune mobilité, 6 équations et 8 inconnues. Le système est hyperstatique d’ordre 2. On peut par exemple utiliser les théorèmes énergétiques pour résoudre le problème. La résolution n’est pas détaillée, mais peut être trouvée ici. Il faut pour cela exprimer l’énergie de déformation totale en fonction de deux inconnues hyperstatiques : YA et MA par exemple. On trouve au terme des calculs :
Dès lors, on peut calculer l’évolution de la déformation εxx sur la peau des lames, côté face plane :
où h=12mm désigne l’épaisseur du capteur.
Comparaison entre modèle analytique et modèle éléments finis
On peut tracer les déformations calculées par le modèle analytique et les comparer à celle obtenues par éléments finis. Les résultats montrent une bonne estimation des valeurs maximales des déformations au droit des perçages : la sensibilité du capteur peut donc être obtenue rapidement par ce calcul, en avant projet. Un modèle analytique dans lequel l’épaisseur des lames est variable fournit quant à lui une très bonne estimation de la valeur maximale, mais également de toutes les valeurs intermédiaires. Il est néanmoins nettement plus compliqué à mettre en place et n’est pas présenté ici. On constate que le modèle éléments finis n’est sans doute pas encore assez fin pour donner la bonne valeur de déformation maximale.
Optimisation de la forme du perçage

Les courbes précédentes montrent une forte dépendance de la déformation mesurée à la position de la jauge (abscisse curviligne). ce point peut être gênant : si on ne maîtrise pas bien la position de la jauge lors du collage, on aura une dépendance de la charge mesurée (traction) à d’autres effets indésirables (moments par exemple). On peut donc se demander s’il existe un profil intérieur qui conduirait à une déformation uniforme dans une zone relativement étendue. Le modèle analytique précédent peut être de nouveau exploité pour résoudre ce problème. On cherche la distribution d’épaisseur telle que la dérivée de la déformation relativement à l’abscisse soit nulle. On trouve :![]()
La comparaison du modèle standard de capteurs (trous circulaires) et du modèle optimisé est présentée ci-dessous. Les calculs sont réalisés par éléments finis dans CATIA. On trouve bien, aux « oscillations numériques » près une valeurs presque uniforme de la déformation au niveau du collage des jauges. Un tel profil rendrait donc le capteur moins sensible à un défaut de positionnement longitudinal des jauges. Il reste le problème de la fabrication…
Comment récupérer l’information mesurée par les jauges ?
Pour estimer la déformation moyenne εxz au niveau de chaque jauge, on introduit quatre « groupes de surfaces par proximité ». En effet, la zone de chaque jauge n’est pas représentée sur la géométrie maillée. Pour cela, on définit quatre surfaces de forme rectangulaire et de taille les dimensions d’une jauge, positionnées aux emplacements des jauges, c’est-à-dire au droit des perçages cylindriques. Les surfaces rectangulaires sont définies dans l’atelier Forme/Generative Shape Design.

Ensuite, il suffit de tracer la composante εxz du tenseur de déformation sur ces zones pour évaluer les quantités mesurées. En pratique, il peut être encore plus facile d’extraire directement les déformations εxz moyennes sur les jauges. Pour cela, on introduit quatre capteurs locaux basés sur le tenseur des déformations correspondant aux quatre groupes précédemment définis. Pour chacun de ces capteurs, on demande d’extraire la composante C11 et de faire la moyenne sur le support, puis de générer un paramètre associé à cette moyenne.
Dans un deuxième temps, on définit un paramètre de type réel qui permet de fournir la quantité représentant le déséquilibre du pont de Wheastone (montage en pont complet) après chargement. On rappelle que le déséquilibre est proportionnel à :![]()
Ces calculs sont effectués pour différents chargements. La composante de traction de l’effort F est toujours égale à 1000 N. Par contre, on introduit des efforts parasites selon x de façon à représenter soit un montage du capteur bi-rotulé avec frottement, soit un montage bi-encastré imposant des efforts parasites de l’ordre de 20% des efforts de traction et des moments parasites selon z de l’ordre de 20% des moments fléchissant maximaux observés dans le modèle simplifié. Les résultats associés sont présentés dans le tableau suivant.

Il montre une dépendance non négligeable des déformations des jauges aux effort et moment parasites si elles sont étudiées séparément. Ainsi, on s’aperçoit qu’il n’est pas judicieux de coller une seule jauge sur le corps d’épreuve, sauf si l’on tolère une erreur de quelques pour cents, ou si la direction des efforts est très bien maîtrisée. Par contre, l’association des quatre jauges en pont complet permet de rendre le montage quasiment indépendant aux efforts parasites. C’est pourquoi ce type de montage est généralement retenu.
