Définition
Un torseur est un champ de vecteurs équiprojectifs.
En mathématique, f est une fonction de ℝ dans ℝ qui à la variable x associe l’image f(x).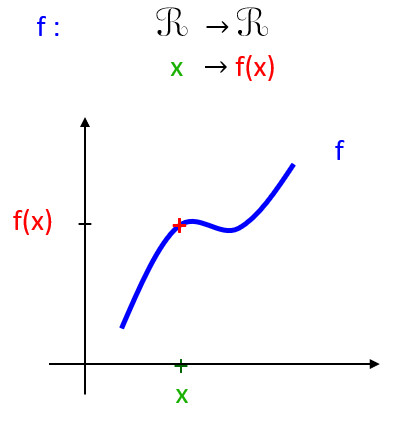 Un torseur \overrightarrow{V}_{2/1} est une fonction (un champ) de ℰ dans E qui à un point A associe un vecteur \overrightarrow{V}_{2/1}(A). Avec ℰ un espace affine et E un espace vectoriel.
Un torseur \overrightarrow{V}_{2/1} est une fonction (un champ) de ℰ dans E qui à un point A associe un vecteur \overrightarrow{V}_{2/1}(A). Avec ℰ un espace affine et E un espace vectoriel.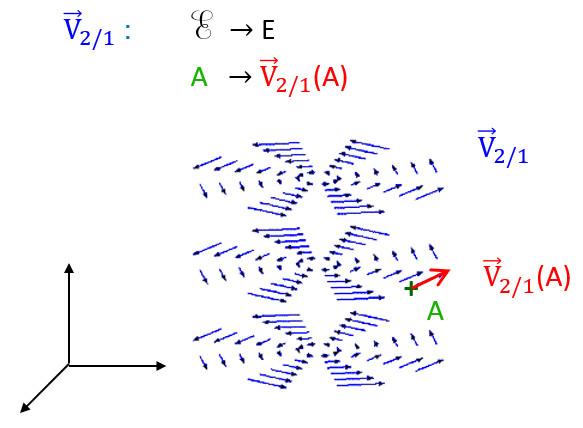
Il y a le même lien entre f et f(x) qu’entre le torseur \overrightarrow{V}_{2/1} et la vitesse \overrightarrow{V}_{2/1}(A).
Notion de champ
A↦f(A) : champ scalaire
A↦\overrightarrow{f}(A) : champ vectoriel
A↦\overline{\overline{f}}(A) : champ tensoriel
\vec{u}↦f(\vec{u}) : opérateur scalaire = forme
\vec{u}↦\overrightarrow{f}(\vec{u}) : opérateur vectoriel
Torseurs particuliers
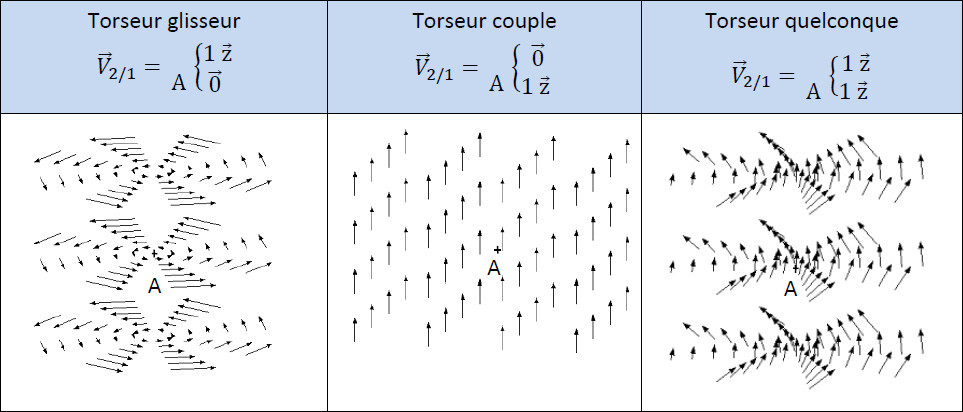
Le mot torseur est de la même famille que le mot torsade dû à la forme de son champ dans le cas général.
On utilise 1 accolade pour définir cette fonction à partir de ses éléments de réduction. De la même manière, on peut définir la fonction exponentielle par exp =\begin{cases} f=f' \\ f(0)=1 \end{cases}
On pourrait cependant utiliser 2 parenthèses, comme pour les coordonnées d’un vecteur. Ou 2 accolades comme pour un ensemble.
S’il y a une ambiguïté, on précise le point à gauche au niveau de la 2nd ligne.
Exemple dans un mécanisme
Prenons l’exemple d’un train simple. Dans un problème de mécanique, on définit une fonction vectorielle différente pour chaque mouvement.
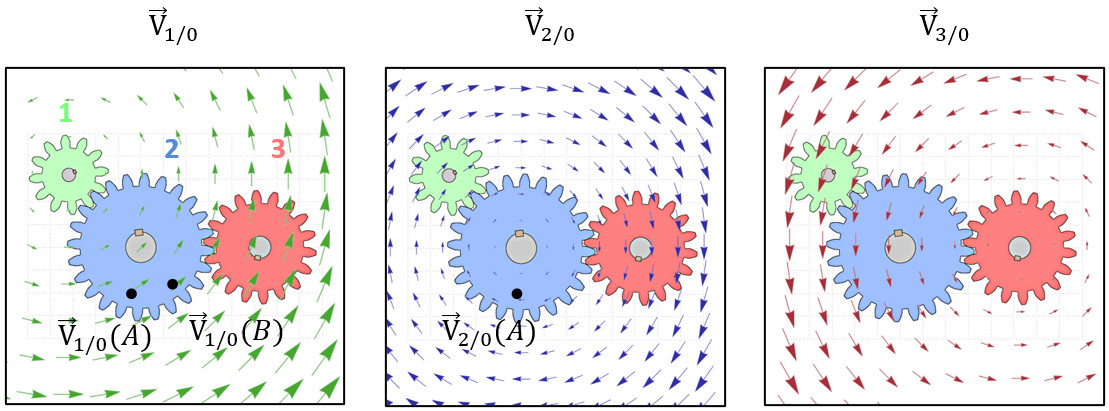
Entre \overrightarrow{V}_{1/0}(A) et \overrightarrow{V}_{1/0}(B) on change le point à mouvement constant : relation de Varignon.
Entre \overrightarrow{V}_{1/0}(A) et \overrightarrow{V}_{2/0}(A) on change de mouvement à point constant : composition des mouvements.
Exemple
Torseur cinématique
\overrightarrow{V}_{i/j} : ℰ → E
A ↦ \overrightarrow{V}_{i/j}(A)
\overrightarrow{V}_{i/j}=\begin{matrix} \\ \\ A \end{matrix}\begin{cases} \overrightarrow{\Omega}_{i/j} \\ \overrightarrow{V}_{i/j}(A) \end{cases}
=\begin{matrix} \\ \\ A \end{matrix}\begin{cases} \omega_{x,i/j}\vec{x}+\omega_{y,i/j}\vec{y}+\omega_{z,i/j}\vec{z} \\ v_{x,i/j}(A)\vec{x}+v_{y,i/j}(A)\vec{y}+v_{z,i/j}(A)\vec{z} \end{cases}=\begin{pmatrix} \omega_{x,i/j} & v_{x,i/j}(A) \\ \omega_{y,i/j} & v_{y,i/j}(A) \\ \omega_{z,i/j} & v_{z,i/j}(A)\end{pmatrix}_{A,(\vec{x},\vec{y},\vec{z})}
\overrightarrow{V}_{i/j}(B)=\overrightarrow{V}_{i/j}(A)+\overrightarrow{BA}∧\overrightarrow{\Omega}_{i/j}
Torseur des actions mécaniques
\overrightarrow{M}_{i→j} : ℰ → E
A ↦ \overrightarrow{M}_{i→j}(A)
\overrightarrow{M}_{i→j}=\begin{matrix} \\ \\ A \end{matrix}\begin{cases} \overrightarrow{R}_{i→j} \\ \overrightarrow{M}_{i→j}(A) \end{cases}
=\begin{matrix} \\ \\ A \end{matrix}\begin{cases} X_{i→j}\vec{x}+Y_{i→j}\vec{y}+Z_{i→j}\vec{z} \\ L_{i→j}(A)\vec{x}+M_{i→j}(A)\vec{y}+N_{i→j}(A)\vec{z} \end{cases}=\begin{pmatrix} X_{i→j} & L_{i→j}(A) \\ Y_{i→j} & M_{i→j}(A) \\ Z_{i→j} & N_{i→j}(A)\end{pmatrix}_{A,(\vec{x},\vec{y},\vec{z})}
\overrightarrow{M}_{i→j}(B)=\overrightarrow{M}_{i→j}(A)+\overrightarrow{BA}∧\overrightarrow{R}_{i→j}
Torseur cinétique
\overrightarrow{\sigma}_{i/j} : ℰ → E
A ↦ \overrightarrow{\sigma}_{i/j}(A)
\overrightarrow{\sigma}_{i/j}=\begin{matrix} \\ \\ A \end{matrix}\begin{cases} \overrightarrow{P}_{i/j} \\ \overrightarrow{\sigma}_{i/j}(A) \end{cases}=\begin{matrix} \\ \\ A \end{matrix}\begin{cases} m\overrightarrow{V}_{i/j}(G) \\ \overline{\overline{I}}_{A,i}.\overrightarrow{\Omega}_{i/j}+\overrightarrow{AG}∧m\overrightarrow{V}_{i/j}(A) \end{cases}
\overrightarrow{\sigma}_{i/j}(B)=\overrightarrow{\sigma}_{i/j}(A)+\overrightarrow{BA}∧m\overrightarrow{V}_{i/j}(G)
Torseur dynamique
\overrightarrow{\delta}_{i/j} : ℰ → E
A ↦ \overrightarrow{\delta}_{i/j}(A)
\overrightarrow{\delta}_{i/j}=\begin{matrix} \\ \\ A \end{matrix}\begin{cases} m\overrightarrow{A}_{i/j}(G) \\ \overrightarrow{\delta}_{i/j}(A) \end{cases}=\begin{matrix} \\ \\ A \end{matrix}\begin{cases} m\overrightarrow{A}_{i/j}(G) \\ \frac{d[\overrightarrow{\sigma}_{i/j}(A)]_{/j}}{dt}+\overrightarrow{V}_{/j}(A)∧m\overrightarrow{V}_{i/j}(G) \end{cases}
\overrightarrow{\delta}_{i/j}(B)=\overrightarrow{\delta}_{i/j}(A)+\overrightarrow{BA}∧m\overrightarrow{A}_{i/j}(G)
Equiprojectivité
Un torseur est un champ équiprojectif (même projection).
2 vecteurs sont équiprojectifs s’ils ont la même projection sur une droite.
Cela veut dire que les points A et B ne peuvent ni se rapprocher, ni s’éloigner.
Exemple
Le champ des vents n’est pas un torseur, c’est un champ qui n’est pas équiprojectif.

Une brique peut être considéré comme un solide indéformable, le champ des vitesses est équiprojectif, c’est donc un torseur.
